Cullen number
In mathematics, a Cullen number is a natural number of the form n · 2n + 1 (written Cn). Cullen numbers were first studied by Fr. James Cullen in 1905. Cullen numbers are special cases of Proth numbers.
Properties
In 1976 Christopher Hooley showed that the natural density of positive integers 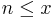 for which Cn is a prime is of the order o(x) for
for which Cn is a prime is of the order o(x) for 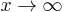 . In that sense, almost all Cullen numbers are composite. Hooley's proof was reworked by Hiromi Suyama to show that it works for any sequence of numbers n · 2n+a + b where a and b are integers, and in particular also for Woodall numbers. The only known Cullen primes are those for n equal:
. In that sense, almost all Cullen numbers are composite. Hooley's proof was reworked by Hiromi Suyama to show that it works for any sequence of numbers n · 2n+a + b where a and b are integers, and in particular also for Woodall numbers. The only known Cullen primes are those for n equal:
- 1, 141, 4713, 5795, 6611, 18496, 32292, 32469, 59656, 90825, 262419, 361275, 481899, 1354828, 6328548, 6679881 (sequence A005849 in OEIS).
Still, it is conjectured that there are infinitely many Cullen primes.
As of August 2009[update], the largest known Cullen prime is 6679881 × 26679881 + 1. It is a megaprime with 2,010,852 digits and was discovered by a PrimeGrid participant from Japan.[1]
A Cullen number Cn is divisible by p = 2n − 1 if p is a prime number of the form 8k - 3; furthermore, it follows from Fermat's little theorem that if p is an odd prime, then p divides Cm(k) for each m(k) = (2k − k) (p − 1) − k (for k > 0). It has also been shown that the prime number p divides C(p + 1) / 2 when the Jacobi symbol (2 | p) is −1, and that p divides C(3p − 1) / 2 when the Jacobi symbol (2 | p) is +1.
It is unknown whether there exists a prime number p such that Cp is also prime.
Generalizations
Sometimes, a generalized Cullen number is defined to be a number of the form n · bn + 1, where n + 2 > b; if a prime can be written in this form, it is then called a generalized Cullen prime. Woodall numbers are sometimes called Cullen numbers of the second kind.
References
- ^ "The Prime Database: 6679881*2^6679881+1", Chris Caldwell's The Largest Known Primes Database, http://primes.utm.edu/primes/page.php?id=89536, retrieved December 22, 2009
Further reading
- Cullen, James (December 1905), "Question 15897", Educ. Times: 534.
- Guy, Richard K. (2004), Unsolved Problems in Number Theory (3rd ed.), New York: Springer Verlag, pp. section B20, ISBN 0387208607.
- Hooley, Christopher (1976), Applications of sieve methods, New York: Cambridge University Press, pp. 115–119, ISBN 0521209153.
- Keller, Wilfrid (1995), "New Cullen Primes", Mathematics of Computation 64 (212): 1733–1741, http://www.ams.org/mcom/1995-64-212/S0025-5718-1995-1308456-3/S0025-5718-1995-1308456-3.pdf.
External links
- Chris Caldwell, The Top Twenty: Cullen primes at The Prime Pages.
- The Prime Glossary: Cullen number at The Prime Pages.
- Weisstein, Eric W., "Cullen number" from MathWorld.
- Cullen prime: definition and status (outdated), Cullen Prime Search is now hosted at PrimeGrid
- Paul Leyland, Generalized Cullen and Woodall Numbers
|
|||||||||||||||||||||||||||||